第133期初中教材配套课件创作
题目要求
| 课题 | 探究四点共圆的条件 |
|---|---|
| 册别 | 人教版本 第 九上 册第 24章 |
| 教材所在页码 | 第119页 |
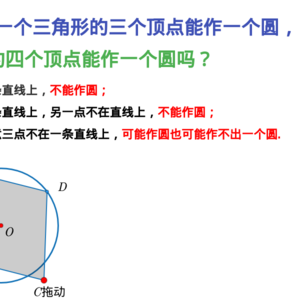
| 教材对应截图 |  |
| 对应的学习目标 | 知道四点共圆的条件及道理。 |
| 教学/学习难点 | 探究过程与方法。 |
| 课件设计说明 | 动画显示探究四点共圆的条件过程,说明探究的思想方法。 |
最优作品
创作者:河北郭根秋(朋友)
(https://www.netpad.net.cn/presentationEditor/presentationPlay.html#posts/4386 )
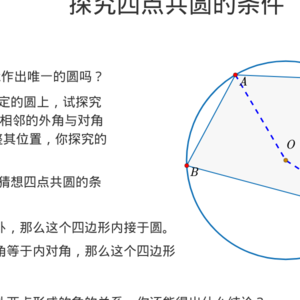
突出优点: 引入简洁,过程自然顺畅。从已知不共线三点确定一个圆入手提出问题:什么条件下不共线的四点能在一个圆上?随后根据已知同弧上的圆周角相等反过来,探究它的逆命题,得出猜想:同侧圆周角相等或异侧圆周角互补,则四点共圆,然后证明,再拓展变换,得出外角等于内对角的四边形是圆内接四边形。
参赛作品
作者:雅安李文录(雅安李文录)
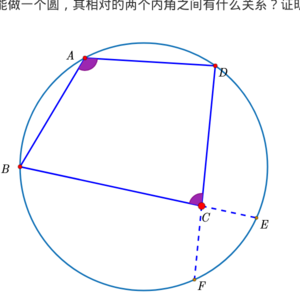
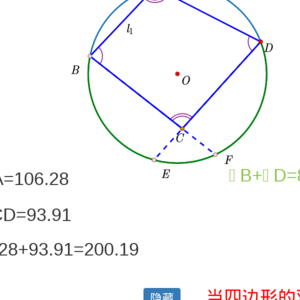
专家点评:明确了过三点可以作一个圆。再提出问题,第四点在这个圆上,探究四边形的对角的数量关系,以及外角与内对角的关系,从而得出结论。有猜想与探究过程。再有一个第四点不在圆上的探究会更好。
作者:吉林张绍明(JCZXZSM001)
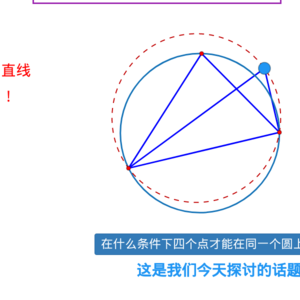
专家点评:一个自由点在由三点确定的圆的平面内自由拖动,从角的度量值,观察探究自由点在圆的外部、内部、圆上三种情况下四边形的对角间的数量关系。
作者:福建刘新和(lxhmyi )
专家点评:四边形的第四个顶点在由三点确定的圆的平面内动画,从角的度量值,观察探究自由点在圆的外部、内部、圆上三种情况下四边形的对角间的数量关系。从而得出正确结论。
作者:河北郭根秋(朋友)
专家点评:文件由六个分页组成。从已知的过不共线三点确定一个圆入手,提出问题:什么条件下不共线的四点能在一个圆上呢?随后把已知的同弧上的圆周角相等反过来,探究它的逆命题,得出猜想
1:立在同一线段同侧的两个三角形,如果这条线段所对的两个角相等,那么,这四个点共圆;继而拓展与联想,得出对顶的两个三角形中,没有共线的两个角相等时,其余四个点共圆。再把已知的圆内接四边形对角互补反过来,探究它的逆命题,得出猜想
2:对角互补的四边形是圆内接四边形;继而拓展与联想,得出外角等于内对角的四边形是圆内接四边形。并给出了小结与证明。
作者:山东王广喜(wangbutian)
专家点评:文件由八个分页组成。来龙1、2、3分别分析了过一点、两点、三点的圆的情况,有分析有结论。继而重点分析探究了过四点有圆还是无圆的情况:先从已经学过的四边形中分析四点共圆的情形;继而又从数的角度对圆内接四边形的性质进行了猜想与证明;接着,倒过来,对对角互补的四边形是圆内接四边形进行了探究与证明。最后总结了探究的方法策略。
作者:吉林田玲(田玲)
专家点评:活页呈现,先对四个点的位置关系分类讨论了四点共圆的的可能。再从已经学过的四边形中分析四点能否共圆的情形,并用测量计算的方法发现四点共圆的四边形对角的数量关系,再倒过来,探究四点共圆的条件并进行了证明。
作者:四川孙国华(老版)
专家点评:活页呈现。先从过一点、两点、三点的圆的情况入手,继而提出问题,过任意一个四边形都有外接圆吗?接着探究了四边形哪些元素决定了过它的四个顶点能作一个圆。对有外接圆的三个四边形进行顶点的拖动变形,观察猜想,提出结论,最后给出了证明。